Net Book Essentials:
The different patterns on each page of Cubes and Things welcome you into the wonderful world of a coloring book, but the good times get even better as you assemble your own geometric shapes! You will be fascinated watching the 2D design fold into a 3D form, and surprised at how easy they are to make.
For years I've been addicted to making these many faceted geometrical forms called polyhedra. And now I have a way to share this delightful creative experience though my new collection of nets. The term 'nets' refers to the different 2D plans, groups of connected polygons (triangles, squares, pentagons, etc), which fold up to become snazzy 3D shapes.
To construct your own polyhedron from a net: cut along the outer edges (keeping it all in one piece), then fold it along the inner edges, and tape it together. Once your form is completed, the next level of enjoyment begins as you contemplate the intriguing symmetries that the pattern creates around the form.
Symmetries in Pattern and Form:
In the center of the five images below is a diagram of an octahedron, which is made up of eight equilateral triangles. The other four pictures are of an octahedron with a pattern from Cubes and Things - Platonics Plus - Net Book #1. Each triangle has the same simple design, but as you rotate it you can see how it changes from different view points. The two pictures on the left show a four-fold symmetry and the two on the right are of a two-fold symmetry. Although I always support whimsical aesthetic additions, coloring these shapes is not only decorative. It emphasizes the different aspects of a shape and its pattern. Does seeing the same view with and without color, give you ideas of how you might color it differently?
You can find plain nets to download for free from a number of different places. Here are links to three good sites:
http://www.mathsisfun.com/geometry/model-construction-tips.html
http://mathgeekmama.com/3-d-shapes-worksheets-free-printables/
http://www.senteacher.org/worksheet/12/NetsPolyhedra.html
Aesthetics Add Meaning:
Most nets only give you the plain shape with low resolution lines. Putting my artistic skills to good use, I've developed nets that make every polyhedron into a special work of art. There is a thin grey line around all the polygon faces that acts as a spacer and a fold line. It accents each polygon face, making sure that every triangle or square is framed nicely to show it off. (Though I sometimes when coloring the net, I darken that grey line to emphasize the edges of the form, as I did with the octahedra above.)
The result is a cool sculpture that looks great wherever you place it around your home, which also teaches you about the shape's geometry. The fun and easily accessible parts of mathematics come from observations into the nature and qualities of an object. There is no need to find time to study, when you learn something of the 2D pattern and 3D form while you were coloring and constructing it —and then even more from looking at or playing with the completed shape!
Physical Details:
The net books are pads of paper glued along the top side for easy removal of whichever shape you want to make next. They are printed on a recycled card stock that feels nice in your hand and has a good flexibility for when you are building the shape, yet the finished form has the right rigidity to show off its fabulous geometry. The eco-friendly company who did the printing is called Greenerprinter. Here is a link to their website:
http://www.greenerprinter.com/grp/
I tried to make every page look lovely to entice you to start working on it. If all you do is color the page, it will still be neat to look at, but the real magic happens when you transform the 2D net into a 3D form. The next images are examples from Cubes and Things - Platonic & Archimedean - Net Book #2:
Net Books #1 & #2:
When I was first sharing my nets, I noticed two main preferences: either people wanted to make a simple shape that didn't take too much time or they asked for the most challenging one I had. In response to this, I compiled two different collections of nets:
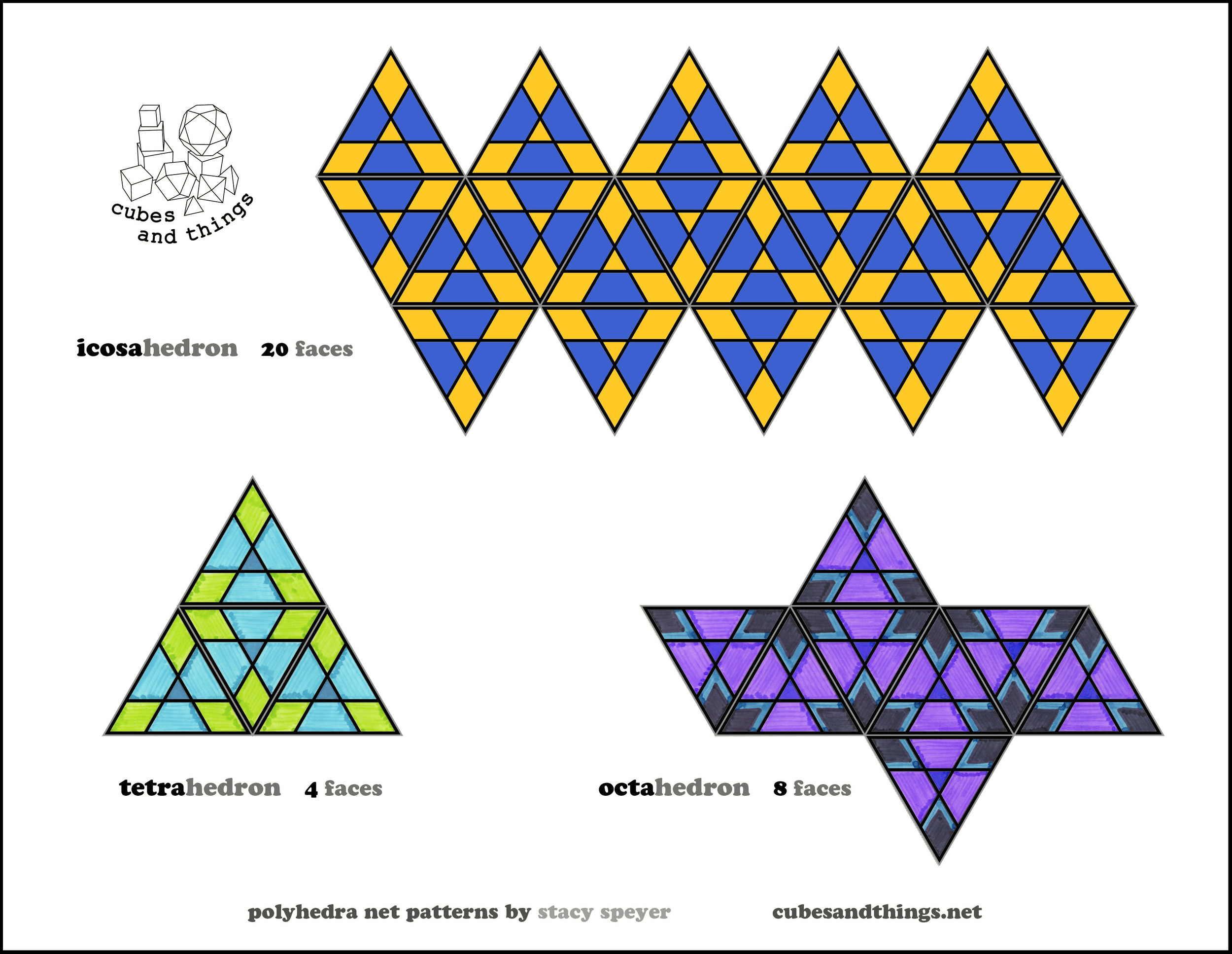
Platonics Plus - Net Book #1 has 28 shapes on 19 pages. There are 10 different kinds of polyhedra. Some are smaller with several nets on 1 page, others fill a page, and a few cover 2 pages.
Platonic & Archimedean - Net Book #2 has 32 shapes on 36 pages. It has the 10 polyhedra that are in Net Book #1, plus 8 more shapes. This net book has twice the pages because the additional shapes are bigger and more complicated.
For those who want to make as many shapes as they can and are thinking of getting both net books, all the polyhedra/pattern combinations in the two net books are unique. Though there are no duplications of a certain pattern on that same polyhedron, some tile designs are seen on several forms. As in the examples above, I was so entranced at how one pattern changed depending on the number of faces meeting at the vertex (mathematicians prefer that term for the corner) of a polyhedron.
The first 6 pages of both books have information about the net books, polyhedra, construction advice, a list of shapes, and a color chart so you can compare the polyhedra in that net book. The color chart of forms in each net book and the list of shapes can be seen in the Cubes and Things store:
http://polyhedra.stacyspeyer.net/to-buy-books
To see charts of the Platonic and Archimedean solids from my book Polyhedra: Eye Candy to Feed the Mind, follow this link:
http://polyhedra.stacyspeyer.net/polyhedra-charts/
For more information about the Platonic and Archimedean Solids follow these links:
https://en.wikipedia.org/wiki/Platonic_solid
https://en.wikipedia.org/wiki/Archimedean_solid
That Tricky Last Piece:
Anyone who has tried to make a polyhedron will know how hard it can be to nicely join up that tricky last piece. An easy solution came to me from my textile background. Most people who work with fabric have a variety of pins around. I found the perfect pin that could help me attach that last piece. Below are the shaded drawings and directions from the net books on how to use the pin:
▪If possible, leave the last piece only connected on one side (m). Put tape on all its remaining sides (with tape on the outside (n) or on the inside (o)). After you carefully press the piece into place, you can no longer apply pressure from the inside. This is when you use the attached pin. Poke it through the vertex and under the edge you are taping (p). Now you can secure the last pieces of tape by pressing your finger down on the outside and, (with the pin) up from the inside.
To start things off right, the first 200 net books will come with an attached pin!
Polyhedra Parties:
Now that the work of completing the net books is done, I want to share this special experience with as many people as I can. Joining in with those looking for new ways to inspire a joy for learning in STEM & STEAM programs, I want to work with schools, summer camps, and after school programs to have Polyhedra Parties!
Polyhedra Parties are the perfect blend of focused play that gently moves towards learning math. The beauty of the shapes can make someone curious to learn a little bit about their geometry. This leads to the kind of thinking involved in understanding how to categorize these different shapes, which can open the door to the enquiring mind that is hungry to learn more. Also, the concepts of symmetry observable in polyhedra are a part of very high level and fascinating mathematical subjects.
If you know of a group in need of a Polyhedra Party (for kids or adults, academically focused or not) and who would like me to lead their event, send me an e-mail at cubesandthings@gmail.com. I can come well supplied with a stack of nets, markers, crayons, scissors, and tape, as well as examples of my art which led to my passion for polyhedra. My years of experience teaching art and my enthusiasm for polyhedra make it an excellent experience. Polyhedra Parties are so much fun!
Thank you for reading this and please let me know what you think of it!
Stacy